RD variables

RD variables

Relative demand, which is the firm demand divided by the industry average demand, will be predicted based on the following variables:

Relative price (Prel): this data set carries pricing information, it is computed by dividing the firm price by the industry average price
Relative advertising (Arel): this data set carries promotion information, it is computed by dividing the firm advertising by the industry average advertising
Last quarter's RD (RD1): this data set carries brand loyalty information, it is computed by dividing last quarter's firm demand by last quarter's industry average demand


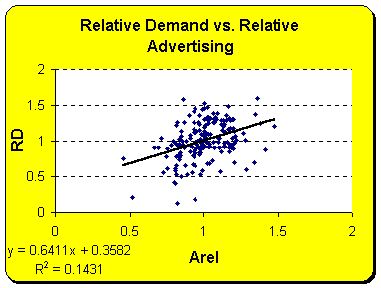
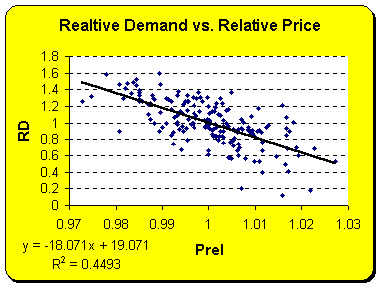
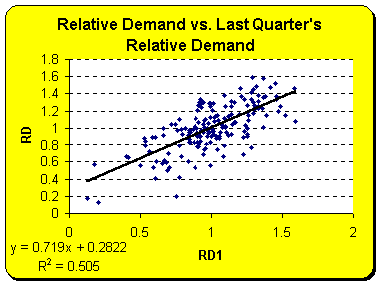
	The scatter plots show that two independent variables do correlate to the dependent variable, which is relative demand. Relative advertising, however, does not correlate to relative demand very much.

A correlation matrix is needed to get a better understanding of the relationship between all of the variables.

	RD	Prel	Arel	RD1
RD	1.000
Prel	-0.495	1.000
Arel	0.382	0.417	1.000
RD1	0.833	-0.248	0.170	1.000

The correlation matrix confirms, that Arel is not very much correlated to RD, in fact it is more correlated to Prel. It can also bee seen, that the independent variables are not highly correlated to each other.

A regression analysis reveals how well RD can be predicted using the independent variables:

Regression Analysis for RD, Using Prel, Arel, and RD1 as Independent Variables

Regression Statistics					It turns out from the regression analysis, that all independent variables are indeed independent, and the coefficients are able to explain roughly 95% of the values of Relative Demand
Multiple R	0.9785
R Square	0.9575
Adj. R Squ.	0.9568
Observations	179

Regression Coefficients
	Coefficients	Stand. Err.	t Stat	P-value
Intercept	16.1300	0.4445	36.2862	0.0000
Prel	-16.4445	0.4441	-37.0255	0.0000
Arel	0.7796	0.0269	28.9347	0.0000
RD1	0.5334	0.0164	32.4615	0.0000

Based on the table above, the following equation can be created:

RD=16.1300-16.4445*Prel+0.7796*Arel+0.5334*RD1

This equation explains roughly 95% of all RD values based on Prel, Arel and RD1.